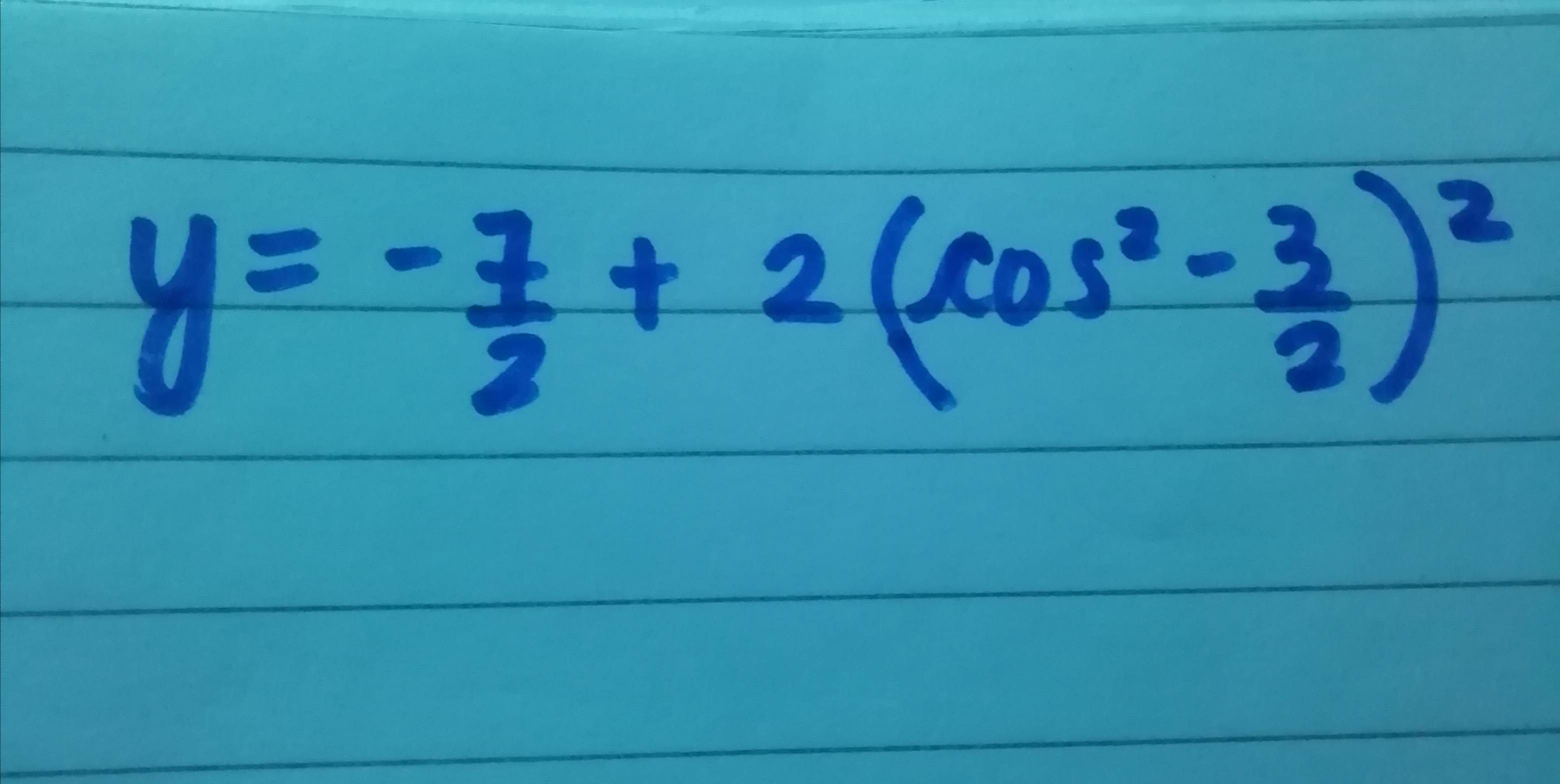In the world of mathematics, understanding how to find the range of a function is a fundamental skill that bridges the gap between equations and real-world applications. The range of a function represents all the possible output values it can produce. Whether you're a student tackling precalculus, a professional working in data modeling, or simply a curious learner, mastering this concept can unlock a deeper appreciation for mathematical relationships.
But what makes finding the range of a function so essential? For starters, it helps us understand the behavior of equations and how they interact with their variables. From quadratic and linear functions to trigonometric and exponential ones, every type of function has unique characteristics that define its range. By knowing the range, you can predict outcomes, solve optimization problems, and even model scenarios in physics, economics, and engineering.
In this comprehensive guide, we will dive deep into the nuances of determining the range of a function. We’ll explore step-by-step methods, practical examples, and even tackle common questions about the topic. By the end, you'll not only know how to find the range of a function but also appreciate the elegance and utility of this mathematical concept.
Read also:Ultimate Guide To Tummy Control Underwear Enhance Your Confidence
Table of Contents
- What Is the Range of a Function?
- Why Is Finding the Range Important?
- Methods to Find the Range
- How to Find Range Using Domain?
- Common Range Determination Methods
- Example 1: Simple Linear Function
- Example 2: Quadratic Function
- Example 3: Trigonometric Function
- Example 4: Exponential Function
- How to Use Graphing to Find Range?
- Range in Real-Life Applications
- Common Mistakes When Finding Range
- How Does Range Differ from Domain?
- Frequently Asked Questions
- Conclusion
What Is the Range of a Function?
The range of a function refers to the complete set of all possible output values that the function can produce. In simpler terms, it’s the collection of all the y-values or dependent variable values you can achieve when plugging every possible x-value (or input) into the function.
For example, consider the function f(x) = x². If you input any real number for x, the output will always be a non-negative number (e.g., 0, 1, 4, 9). Hence, the range of this function is all non-negative real numbers, or in mathematical notation: [0, ∞).
Why Is Finding the Range Important?
Understanding the range of a function has a wide range of applications, from solving equations to modeling real-world problems. Here are a few reasons why it's crucial:
- Predicting Outcomes: Knowing the range helps predict the behavior of a function under specific conditions.
- Optimizing Solutions: In fields like economics and engineering, the range can help identify the best possible outcomes or solutions.
- Understanding Limits: The range gives insight into the boundaries of what a function can achieve, which is essential in calculus and advanced mathematics.
- Application in Graphing: When graphing functions, the range provides information on the vertical span of the graph.
Ultimately, finding the range equips you with a deeper understanding of mathematical behavior and enhances your problem-solving toolkit.
Methods to Find the Range
There are multiple ways to determine the range of a function, depending on the type of equation you're dealing with. These methods include:
- Using the function's domain.
- Analyzing the function's equation algebraically.
- Using derivatives to find critical points (for calculus-based approaches).
- Graphing the function and observing the output values.
In the sections below, we’ll dive deeper into these techniques with examples and step-by-step instructions.
Read also:Dining At Its Finest Jonathans Grille Experience
How to Find Range Using Domain?
To find the range using the domain of a function, you need to understand the relationship between inputs and outputs. The domain represents all possible x-values you can input into the function, and by substituting these x-values into the function, you can determine the corresponding y-values, which form the range.
Steps to Find the Range Using Domain
- Identify the domain of the function (all permissible input values).
- Substitute these input values into the function.
- Record all possible output values (y-values).
- Combine these y-values to determine the range.
For instance, in the function f(x) = √x, the domain is [0, ∞), since you can’t take the square root of a negative number. Substituting values from the domain into the function gives output values ranging from 0 to infinity. Therefore, the range is [0, ∞).
Common Range Determination Methods
There are several common methods mathematicians and students use to determine the range of a function. These include:
1. Algebraic Manipulation
Rewriting the function to express x in terms of y can help identify the range. For example:
- Given f(x) = x², rewriting it gives y = x² or x = ±√y.
- The output y must be non-negative, so the range is [0, ∞).
2. Graphical Analysis
By sketching or plotting the graph of a function, you can visually identify the vertical span of the graph, which corresponds to the range.
3. Derivatives (For Calculus Students)
Using derivatives, you can find critical points of a function to determine its maximum and minimum values, which can help identify the range.
Example 1: Simple Linear Function
Consider the linear function f(x) = 2x + 3. Since linear functions have no restrictions on their domain or range, the range of this function is all real numbers.
Example 2: Quadratic Function
Quadratic functions, such as f(x) = x², typically have a parabolic shape. In this case, the range is limited to non-negative values, as mentioned earlier.
Example 3: Trigonometric Function
For periodic functions like sin(x) or cos(x), the range is generally restricted. For example, the range of sin(x) is [-1, 1].
Example 4: Exponential Function
Exponential functions, such as f(x) = e^x, have a range of (0, ∞), as their outputs are always positive.
How to Use Graphing to Find Range?
Graphing is a powerful tool for finding the range of a function. By visually analyzing the graph, you can identify the lowest and highest points (or lack thereof) to determine the range.
Range in Real-Life Applications
The concept of range is widely used in various fields, from physics to economics. For example, in physics, the range of a projectile's motion can help determine its maximum height and distance.
Common Mistakes When Finding Range
Some common errors include:
- Ignoring domain restrictions.
- Misinterpreting the graph.
- Overlooking negative values in the output.
How Does Range Differ from Domain?
While the domain refers to all possible input values, the range focuses on the output values. Understanding both is crucial for fully analyzing a function.
Frequently Asked Questions
1. What is the range of a constant function?
The range of a constant function is a single value, as the output doesn’t change regardless of the input.
2. Can a function have an infinite range?
Yes, functions like linear functions can have an infinite range, spanning all real numbers.
3. How do you find the range of a rational function?
Analyze the numerator and denominator to identify restrictions and use algebraic manipulation or graphing.
4. What is the range of the logarithmic function?
The range of log(x) is (-∞, ∞), as it can take any real value.
5. Can a range include negative values?
Yes, depending on the function. For example, f(x) = -x² has a range of (-∞, 0].
6. Is the range always a continuous interval?
No, some functions, like piecewise or discrete functions, may have a non-continuous range.
Conclusion
Mastering how to find the range of a function is an essential mathematical skill that has applications far beyond the classroom. Whether you’re solving equations, graphing, or modeling real-world scenarios, understanding the range allows for better predictions, optimizations, and interpretations. By applying the methods and examples discussed, you can confidently tackle any range-related problem and deepen your appreciation for the beauty of mathematics.
Article Recommendations