What Is Cosecant: A Complete Guide To This Essential Trigonometric Function

Cosecant is one of the six fundamental trigonometric functions that play a pivotal role in mathematics, specifically in the study of triangles and periodic phenomena. Often abbreviated as csc, the cosecant function is the reciprocal of the sine function. While it may not be as commonly used as sine or cosine in everyday applications, its importance in advanced mathematics, engineering, and physics cannot be overstated.

At its core, cosecant helps us understand relationships between angles and side lengths in right-angled triangles. If you've ever wondered how we calculate the steepness of a slope or the behavior of waves, trigonometric functions like cosecant are the unsung heroes of these calculations. By focusing on the reciprocal relationship with sine, cosecant extends our ability to model and solve real-world problems involving oscillations, circular motion, and much more.

In this article, we’ll explore “what is cosecant” in comprehensive detail. From its mathematical definition to its applications in various fields, we’ll break down every aspect of this intriguing function. Whether you're a student, educator, or professional, this guide will provide clear insights into the world of cosecant and its significance in trigonometry. Let’s dive in!

Read also:

Expert Guide To Planting Dahlia Tubers Tips For A Stunning Garden

Table of Contents

1. What Is the Definition of Cosecant?
2. Mathematical Notation and Reciprocal Nature
3. How Is Cosecant Calculated?
4. Real-World Applications of Cosecant
5. Why Is Cosecant Important?
6. Graphing the Cosecant Function
7. What Are the Properties of Cosecant?
8. Cosecant in Right-Angled Triangles
9. Difference Between Cosecant and Other Functions
10. Common Mistakes When Using Cosecant
11. Relationship With Other Trigonometric Functions
12. How Does Cosecant Relate to the Unit Circle?
13. Frequently Asked Questions About Cosecant
14. Practical Tips for Learning Cosecant
15. Conclusion

What Is the Definition of Cosecant?

The term "cosecant" originates from the Latin phrase "complementi secant," which translates to "the secant of the complement." Cosecant is defined as the reciprocal of the sine function. Mathematically, this means:

csc(θ) = 1/sin(θ)

Here, θ (theta) represents an angle in a right-angled triangle or within the unit circle. It’s important to note that the cosecant function is undefined when the sine of an angle equals zero. This occurs at specific points, such as 0°, 180°, 360°, and so forth, where the sine function reaches a value of zero.

Unlike sine and cosine, which are bounded between -1 and 1, the cosecant function can take on any value greater than or equal to 1 or less than or equal to -1. This property makes it particularly useful in scenarios requiring the measurement of extreme oscillations or steep inclines.

Mathematical Notation and Reciprocal Nature

Cosecant is represented by the abbreviation csc, followed by the angle in parentheses. For example, the cosecant of a 45-degree angle is written as csc(45°). This compact notation makes it convenient to use in equations and formulas.

Being the reciprocal of sine, the cosecant function shares a unique relationship with its counterpart. To illustrate:

Read also:

Who Wrote And Sang The Song Costumbres Exploring The Origins And Impact

• If sin(θ) = 0.5, then csc(θ) = 1/0.5 = 2.
• If sin(θ) = -0.5, then csc(θ) = 1/(-0.5) = -2.

This reciprocal nature simplifies many trigonometric calculations, particularly when working with ratios or inverses. Moreover, the cosecant function is periodic, meaning it repeats its values over a fixed interval. In the case of cosecant, this period is 360° or 2π radians.

How Is Cosecant Calculated?

What are the steps to find cosecant?

To calculate cosecant, follow these steps:

1. Determine the angle θ for which you want to find the cosecant.
2. Calculate the sine of θ using a calculator, trigonometric table, or unit circle.
3. Take the reciprocal of the sine value. This means dividing 1 by the sine of θ.

For example, let’s find csc(60°):

• Step 1: sin(60°) = √3/2 (using a trigonometric table).
• Step 2: csc(60°) = 1/(√3/2) = 2/√3 = 2√3/3 after rationalizing the denominator.

These steps provide a straightforward way to compute cosecant for any angle, provided the sine value is not zero.

Can you calculate cosecant without a calculator?

Yes, you can calculate cosecant without a calculator for common angles like 30°, 45°, and 60° by using trigonometric tables or the unit circle. Memorizing the sine values for these angles simplifies the process.

Real-World Applications of Cosecant

While cosecant may seem abstract, it has numerous practical applications in various fields:

• Engineering: Cosecant is used in the design of mechanical systems, such as pendulums and oscillators, to calculate extreme values of motion.
• Physics: In wave mechanics, cosecant helps model the behavior of light and sound waves.
• Architecture: Architects use cosecant to determine the optimal steepness of roofs and ramps.
• Astronomy: The function aids in calculating distances and angles between celestial objects.

These examples underscore the versatility and importance of cosecant in solving real-world problems.

Why Is Cosecant Important?

Cosecant is vital because it extends our understanding of trigonometric relationships. By focusing on the reciprocal of sine, it provides a complementary perspective that enhances problem-solving capabilities. Additionally, cosecant plays a key role in advanced mathematical concepts, such as Fourier analysis and signal processing.

Moreover, its unique properties make it essential for dealing with extreme values. For instance, in engineering, cosecant can model the behavior of structures under stress, offering insights into their limits and stability.

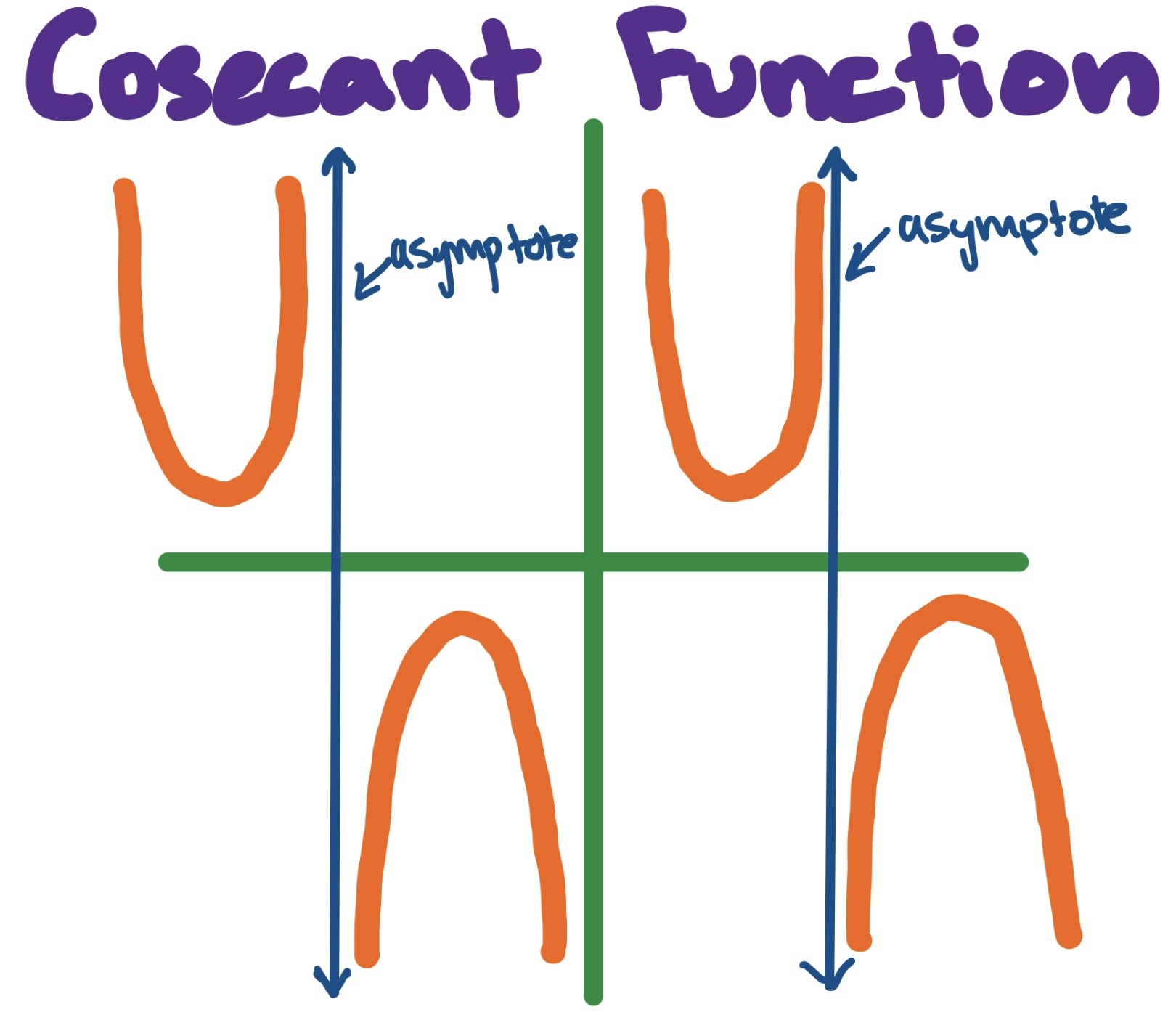
Graphing the Cosecant Function

The graph of the cosecant function features a series of upward and downward curves, with vertical asymptotes at angles where sine equals zero. These asymptotes represent the points where cosecant is undefined. The graph’s periodic nature makes it an excellent tool for modeling cyclic phenomena.

To graph cosecant:

1. Plot the sine function as a reference.
2. Take the reciprocal of each sine value to create the cosecant curve.
3. Add vertical asymptotes at angles where sine equals zero.

What Are the Properties of Cosecant?

Cosecant has several unique properties:

• It is undefined at angles where sine equals zero.
• Its values are always greater than or equal to 1 or less than or equal to -1.
• It is a periodic function with a period of 360° or 2π radians.
• It has vertical asymptotes at multiples of 180° or π radians.

These properties make cosecant a fascinating subject of study and a powerful mathematical tool.

Frequently Asked Questions About Cosecant

What is the difference between sine and cosecant?

Sine is a primary trigonometric function, while cosecant is its reciprocal. Cosecant is undefined when sine equals zero.

Why is cosecant undefined at certain angles?

Cosecant is undefined at angles where sine equals zero because dividing by zero is mathematically invalid.

Is cosecant always positive?

No, cosecant can be positive or negative depending on the angle's quadrant in the unit circle.

How does cosecant relate to the unit circle?

Cosecant is the reciprocal of sine, which corresponds to the y-coordinate of a point on the unit circle.

What are the applications of cosecant in real life?

Cosecant is used in fields like engineering, physics, and architecture to solve problems involving extreme values and oscillations.

Can cosecant be used with non-right triangles?

Yes, but it typically requires additional steps, such as using the Law of Sines, to calculate side lengths or angles.

Practical Tips for Learning Cosecant

Here are some tips to master cosecant:

• Practice calculating cosecant for various angles using a unit circle.
• Memorize sine values for common angles like 30°, 45°, and 60°.
• Understand the relationship between sine and cosecant to simplify calculations.
• Use graphing tools to visualize the cosecant function and its properties.

Conclusion

In summary, cosecant is a fundamental trigonometric function that offers unique insights into the relationships between angles and side lengths. Whether you're studying right-angled triangles, analyzing wave patterns, or solving advanced mathematical problems, understanding "what is cosecant" is essential. By mastering its properties, applications, and graphing techniques, you’ll unlock new possibilities in mathematics and beyond.