The concept of the moment of inertia point mass is a cornerstone in the study of physics and mechanics, playing a pivotal role in understanding how mass is distributed and how it influences rotational motion. Engineers, physicists, and educators alike rely on this principle to design systems, solve real-world problems, and teach fundamental scientific concepts. Whether you're delving into the depths of mechanical engineering or simply curious about rotational dynamics, the moment of inertia point mass serves as a critical starting point.
When we talk about rotational motion, the moment of inertia is essentially the rotational equivalent of mass in linear motion. It dictates how a mass resists rotational acceleration around a specific axis, making it an indispensable factor in calculating torque and angular velocity. The moment of inertia point mass, in particular, simplifies this concept by focusing on a single point where all the mass is concentrated, making it easier to analyze complex systems.
This article seeks to demystify the concept of the moment of inertia point mass by breaking it down into manageable sections. From its mathematical derivation to its practical applications, we'll cover everything you need to know. By the end, you'll have a firm grasp of this foundational concept, enabling you to apply it to both academic and professional pursuits. Let's dive into this fascinating topic!
Read also:Empowering Communities Through The Tony Stewart Foundation
Table of Contents
- What is Moment of Inertia Point Mass?
- Why is Moment of Inertia Important?
- Understanding the Formula
- How Does Mass Distribution Affect It?
- Moment of Inertia of a Point Mass in Rotational Motion
- What Are the Units of Moment of Inertia?
- Applications in Physics and Engineering
- Moment of Inertia vs. Mass: What’s the Difference?
- Moment of Inertia in Different Systems
- Moment of Inertia Point Mass in the Real World
- How Do You Calculate It?
- Common Misconceptions About Moment of Inertia
- Historical Context Behind Moment of Inertia
- FAQs
- Conclusion
What is Moment of Inertia Point Mass?
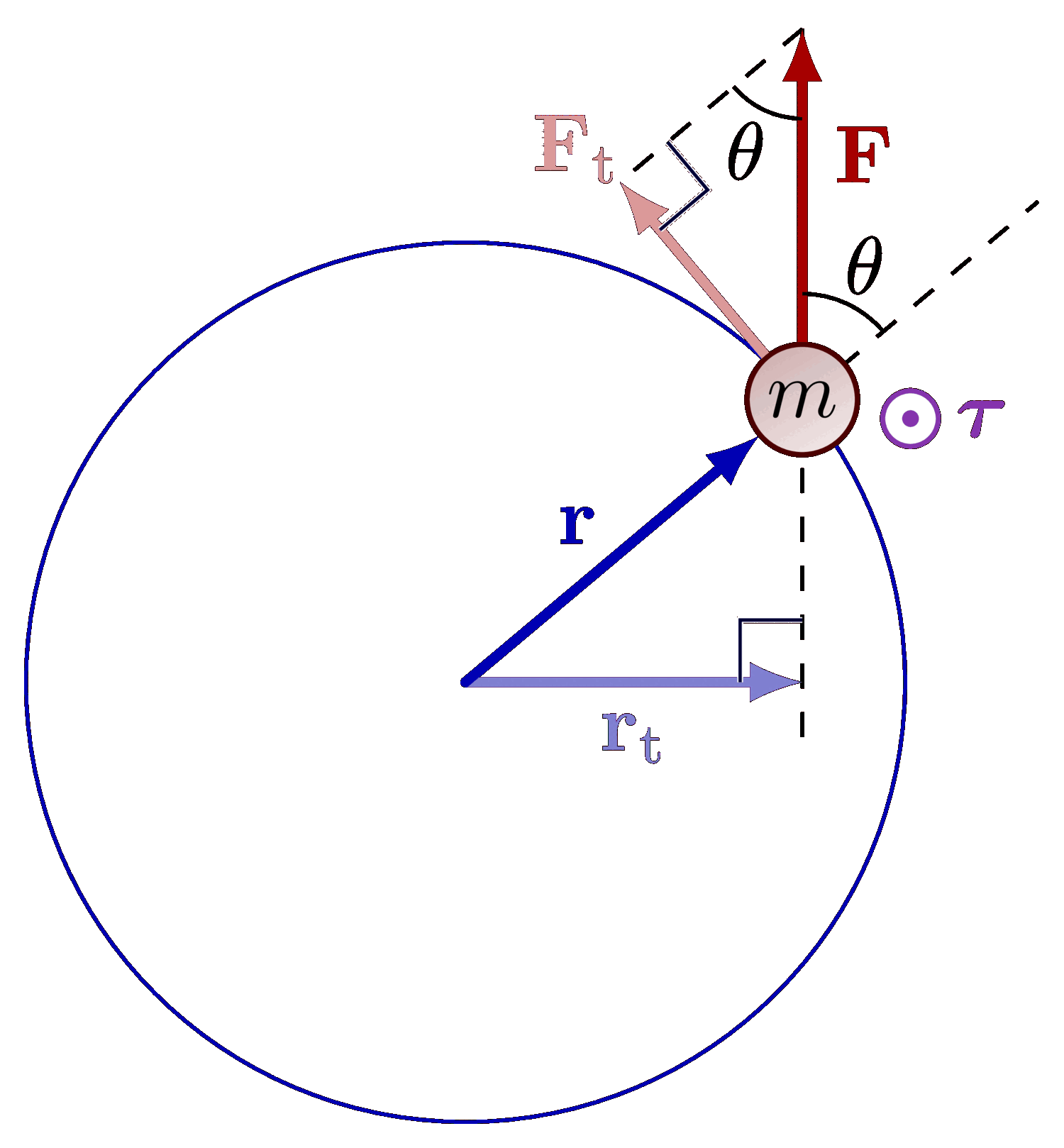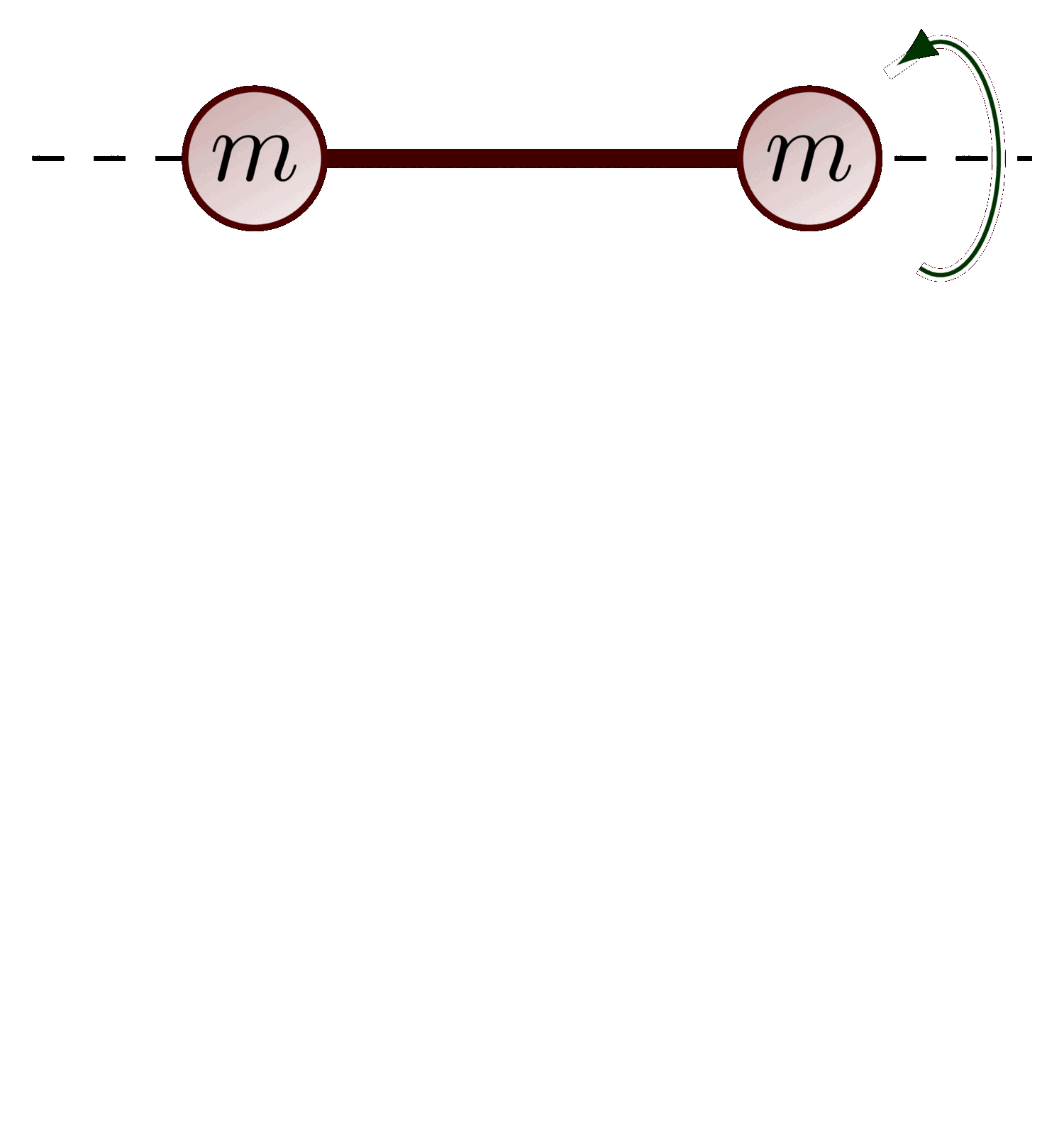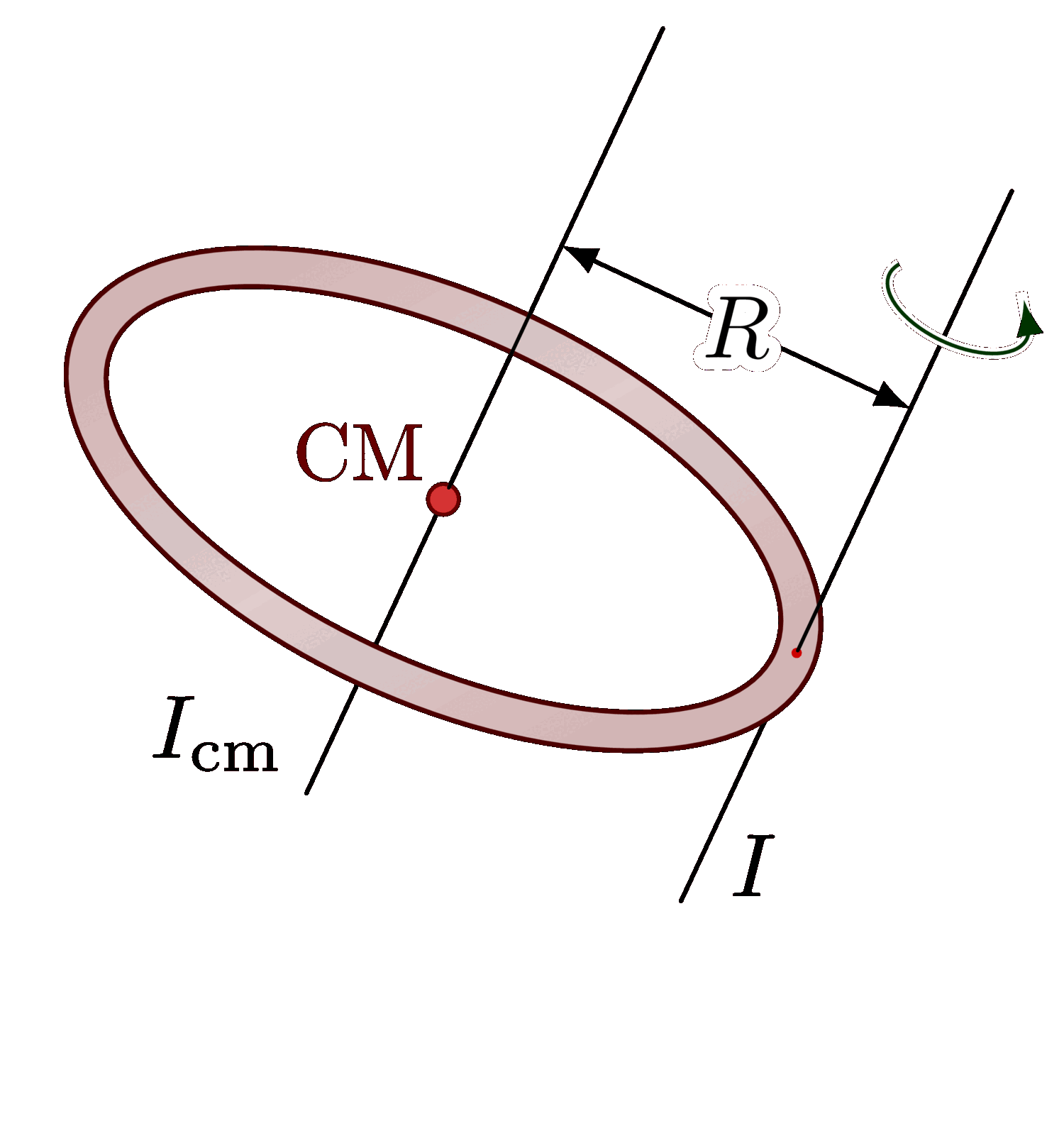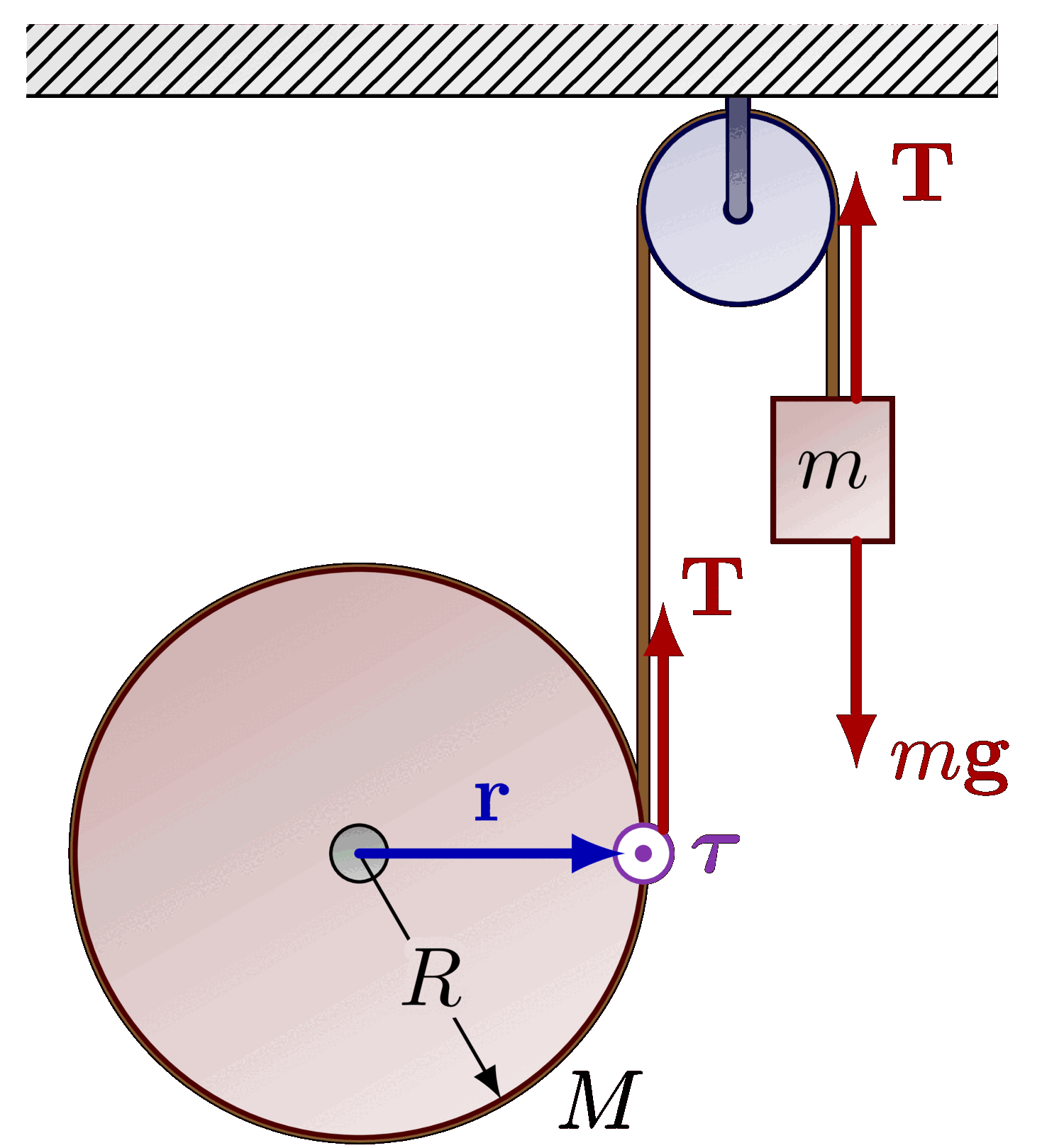
The moment of inertia point mass is a simplified concept used to understand rotational motion in systems where all the mass is considered to be concentrated at a single point. This idealization allows us to focus on the relationship between mass, distance from the axis of rotation, and the resistance to changes in rotational motion. The formula for the moment of inertia of a point mass is given as:
I = m * r², where:
- I = Moment of inertia
- m = Mass of the object
- r = Distance from the axis of rotation
This equation highlights the dependency of rotational inertia on both the mass of the object and its distribution relative to the axis of rotation. Even though it’s a simplified model, it is widely applicable for introductory physics problems and serves as a building block for more complex scenarios.
Why is Moment of Inertia Important?
How does it impact rotational motion?
The moment of inertia determines how much torque is required to achieve a desired angular acceleration for a rotating object. A higher moment of inertia means the object resists changes in rotational speed more strongly. This property is crucial in designing systems like flywheels, gears, and turbines, where efficiency and stability are paramount. Understanding this principle is also vital for analyzing the dynamics of celestial objects, such as planets and stars.
What are the implications in engineering?
In engineering applications, the moment of inertia helps in designing structures and mechanisms that can withstand rotational forces. For instance, it determines the stability of bridges under wind loads or the safety of vehicles taking sharp turns. Engineers often calculate the moment of inertia to ensure that systems are both efficient and secure.
Understanding the Formula
The formula I = m * r² may appear simple, but its implications are profound. It shows that the moment of inertia increases quadratically with the distance from the axis of rotation. This means that even small changes in the distribution of mass can significantly impact the moment of inertia. Let’s break down the components of the formula:
Read also:Secrets Of Kaitlyn Clarks Personal Life Who Is Her Boyfriend
- Mass (m): The total mass of the object.
- Distance (r): The perpendicular distance from the axis of rotation to the point mass.
By understanding these components, you can calculate the moment of inertia for various configurations, ranging from simple point masses to complex rigid bodies.
How Does Mass Distribution Affect It?
Why does distance matter?
The farther a mass is from the axis of rotation, the greater its contribution to the moment of inertia. This is because the distance is squared in the formula. For example, doubling the distance from the axis quadruples the moment of inertia, emphasizing the importance of mass distribution in rotational dynamics.
What happens in irregular systems?
In irregular systems where mass is not uniformly distributed, the moment of inertia is calculated by summing the contributions of all individual point masses. This approach allows for precise calculations in systems with complex geometries, such as spacecraft or robotic arms.
Moment of Inertia of a Point Mass in Rotational Motion
...
What Are the Units of Moment of Inertia?
...
Applications in Physics and Engineering
...
Moment of Inertia vs. Mass: What’s the Difference?
...
Moment of Inertia in Different Systems
...
Moment of Inertia Point Mass in the Real World
...
How Do You Calculate It?
...
Common Misconceptions About Moment of Inertia
...
Historical Context Behind Moment of Inertia
...
FAQs
Below are some common questions related to the moment of inertia point mass:
- What is the difference between moment of inertia and torque? Torque refers to the force causing rotational motion, while the moment of inertia measures the resistance to that motion.
- Can the moment of inertia be negative? No, the moment of inertia is always a non-negative value as it depends on mass, which cannot be negative.
- Does the moment of inertia change with speed? No, it depends solely on the mass and its distribution, not the speed of rotation.
- What is the significance of the axis of rotation? The axis of rotation determines the distance (r) in the formula, significantly affecting the moment of inertia.
- How is the moment of inertia used in space exploration? It helps in designing spacecraft to ensure stability and precise control during rotations.
- Is the moment of inertia the same for all shapes? No, different shapes and mass distributions have unique moments of inertia.
Conclusion
The moment of inertia point mass is more than just a theoretical concept—it is an essential tool in both scientific and practical applications. By grasping its principles, you can unlock a deeper understanding of rotational dynamics, enabling you to tackle challenges in physics, engineering, and beyond. Whether you're a student, a professional, or simply an enthusiast, the insights gained here provide a strong foundation for further exploration.
Article Recommendations