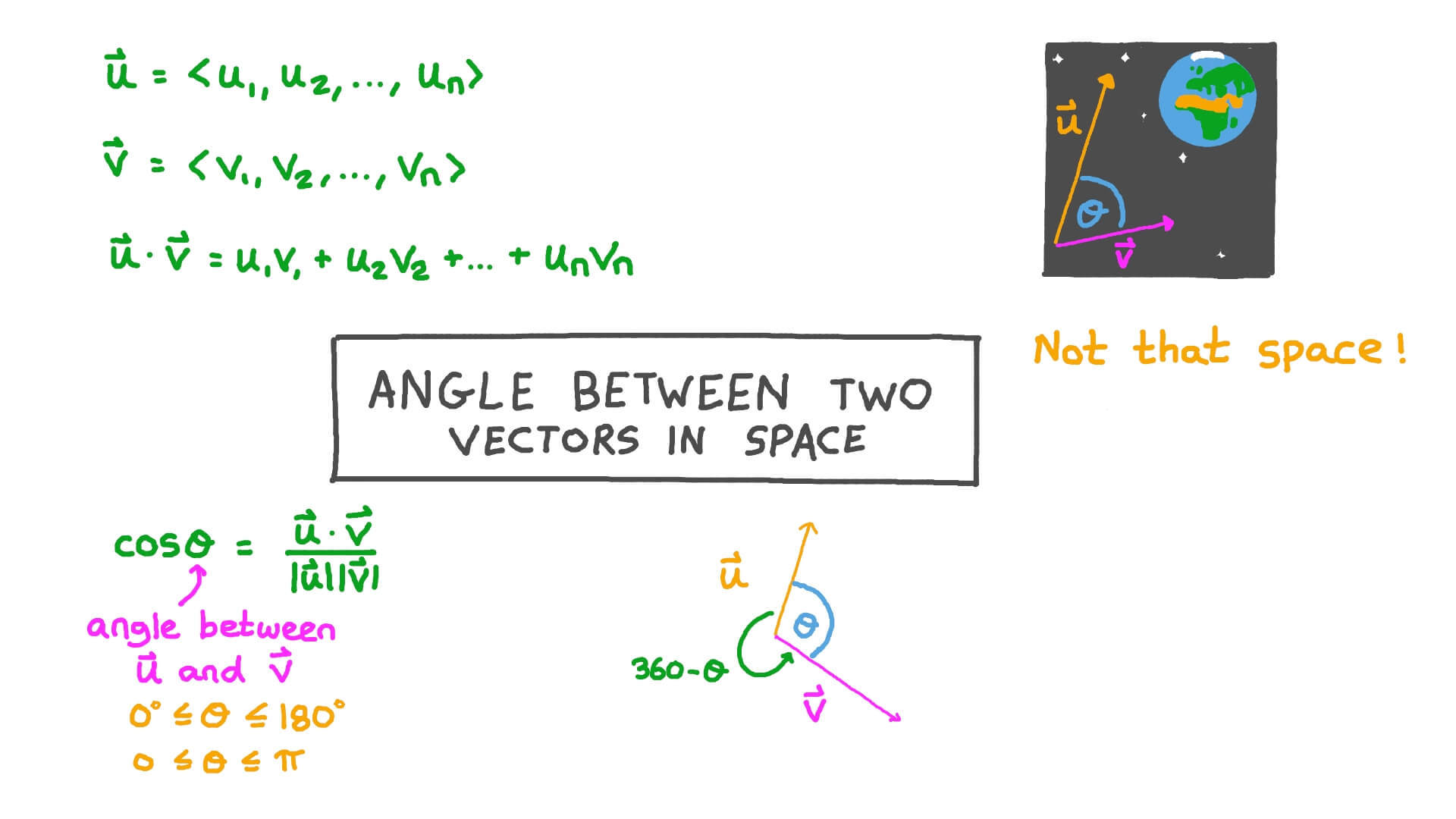Mastering The Calculation: How To Get Angle Between Two Vectors

In the world of mathematics and physics, vectors are indispensable tools that help us understand the direction and magnitude of quantities. Calculating the angle between two vectors is a fundamental operation used in diverse fields such as computer graphics, engineering, robotics, and even machine learning. This process plays a pivotal role in determining the relationship between two entities in multi-dimensional space, enabling precise problem-solving and analysis.

When we talk about vectors, we are referring to quantities that possess both magnitude and direction. For instance, forces, velocities, and accelerations are all examples of vectors. Understanding the angle between two vectors is particularly valuable because it sheds light on how closely aligned or divergent these quantities are. Whether you're designing the trajectory of a robotic arm or simulating physics in a video game, mastering this calculation can significantly enhance your skill set.

In this detailed guide, we’ll walk you through everything you need to know about how to get the angle between two vectors. From the mathematical formula and applications to practical examples and tools, this article has been meticulously designed to help you grasp the concept in-depth. By the end, you’ll not only understand the theory but also have the confidence to apply it in real-world scenarios. Let’s dive in!

Read also:

Ultimate Guide To The Stylish And Quirky Easy Bake Coven Shirt

Table of Contents

• Understanding Vectors and Their Importance
• What Is the Angle Between Two Vectors?
• Why Is It Important to Get Angle Between Two Vectors?
• The Mathematical Formula
• Step-by-Step Guide to Calculate Angle Between Two Vectors
• Applications in Different Fields
• Tools and Software to Get Angle Between Two Vectors
• Common Mistakes to Avoid
• How Does Dot Product Help in Vector Calculations?
• What If Vectors Are in 3D Space?
• Examples of Angle Calculations
• Frequently Asked Questions
• Conclusion and Key Takeaways

Understanding Vectors and Their Importance

Vectors are mathematical entities defined by both a magnitude (how much) and a direction (which way). Unlike scalar quantities, which are only concerned with magnitude, vectors allow us to describe phenomena in a more comprehensive way. For example, a car traveling at 60 miles per hour towards the north is best represented by a vector, as it includes both speed and direction.

Vectors have become essential in various fields, including physics, engineering, computer graphics, and more. They allow precise representation of forces, movements, and alignments in systems. Understanding how vectors interact, particularly the angle between them, is a cornerstone of solving complex problems in multi-dimensional spaces.

What Is the Angle Between Two Vectors?

The angle between two vectors is defined as the measure of rotation required to align one vector with another. It is typically measured in degrees or radians and falls within the range of 0° to 180°. The smaller the angle, the more aligned the vectors are; the larger the angle, the more divergent they are.

To calculate this angle, the dot product of the vectors and the magnitudes of the vectors are used. The dot product essentially measures the extent to which two vectors point in the same direction, while the magnitudes quantify their lengths. Together, these values form the basis of the formula to calculate the angle.

Why Is It Important to Get Angle Between Two Vectors?

Determining the angle between two vectors is critical for understanding their relationship. This has practical implications in:

• Physics: Calculating angles helps in analyzing force interactions and energy transfers.
• Computer Graphics: It is used to simulate lighting, shading, and object alignment.
• Engineering: Understanding the interaction between forces acting on a structure.
• Robotics: Defining joint movements and trajectories.

Without this calculation, many real-world applications would lack precision, leading to inefficiencies or errors.

Read also:

Tawny Kitaen Cause Of Death A Look Into The Life And Legacy

The Mathematical Formula

The formula to get the angle between two vectors is derived from the dot product. It is expressed as:

θ = cos-1((A · B) / (||A|| ||B||))

Here’s what each term means:

• A · B: The dot product of vectors A and B.
• ||A||: The magnitude (length) of vector A.
• ||B||: The magnitude (length) of vector B.
• θ: The angle between the two vectors in radians or degrees.

Step-by-Step Guide to Calculate Angle Between Two Vectors

Follow these steps to calculate the angle between two vectors:

1. Find the dot product: Compute the scalar product of the two vectors.
2. Calculate magnitudes: Determine the magnitude of each vector.
3. Apply the formula: Use the formula θ = cos-1((A · B) / (||A|| ||B||)) to find the angle.
4. Convert to degrees: If required, convert the angle from radians to degrees using the formula θ(degrees) = θ(radians) × (180/π).

Each step involves straightforward mathematical operations, making this calculation accessible to anyone with a basic understanding of algebra and trigonometry.

Applications in Different Fields

The ability to get the angle between two vectors has wide-ranging applications:

• Physics: Used in mechanics to analyze force vectors and motion.
• Computer Graphics: Critical for rendering 3D models and animations.
• Robotics: Helps in programming precise movements and rotations.
• Machine Learning: Used in similarity measures for high-dimensional data.

These examples underscore the versatility and importance of this mathematical operation.

Tools and Software to Get Angle Between Two Vectors

Several tools and software can simplify the process of calculating angles between vectors, such as:

• MATLAB: A powerful tool for mathematical computations.
• Python Libraries: Libraries like NumPy and SciPy offer straightforward functions for vector calculations.
• Online Calculators: Free resources available for quick calculations.

Leveraging these tools can save time and reduce the likelihood of errors.

Common Mistakes to Avoid

While calculating the angle between two vectors, avoid the following mistakes:

• Using incorrect vector magnitudes.
• Failing to normalize vectors when required.
• Misinterpreting the results (e.g., radians vs degrees).

Attention to detail is key to accurate calculations.

How Does Dot Product Help in Vector Calculations?

The dot product is a cornerstone of vector mathematics. It provides a scalar value that reflects the alignment of two vectors. In angle calculations, it serves as a bridge between the vectors’ magnitudes and their relative orientation.

What If Vectors Are in 3D Space?

Calculating the angle between vectors in 3D space follows the same principles but requires additional computational effort. The formula remains applicable, but the vectors must be accurately defined with three components each.

Examples of Angle Calculations

Let’s consider two vectors A = (3, 4) and B = (4, 3):

1. Calculate dot product: A · B = (3)(4) + (4)(3) = 24.
2. Find magnitudes: ||A|| = √(3² + 4²) = 5, ||B|| = √(4² + 3²) = 5.
3. Apply formula: θ = cos-1(24 / (5 × 5)).
4. Result: θ ≈ 36.87°.

This example illustrates the simplicity of the process.

Frequently Asked Questions

1. What is the formula to get the angle between two vectors?

   The formula is θ = cos-1((A · B) / (||A|| ||B||)).

2. What tools can I use to calculate angles?

   Tools like MATLAB, Python libraries (NumPy), and online calculators can be helpful.

3. Can the angle be negative?

   No, the angle between two vectors is always between 0° and 180°.

4. What if the vectors are perpendicular?

   If vectors are perpendicular, their dot product is zero, and the angle is 90°.

5. How do I handle angles in 3D space?

   The same formula applies, but ensure the vectors are correctly defined with three components.

6. Why is the angle important in machine learning?

   It helps in calculating similarity measures like cosine similarity.

Conclusion and Key Takeaways

Understanding how to get the angle between two vectors is an essential skill for anyone working with mathematics, physics, or computer science. By mastering this calculation, you unlock the ability to analyze relationships between quantities in multi-dimensional spaces. From theory to practical applications, this guide provides everything you need to excel in this area. So, roll up your sleeves, apply these principles, and take your problem-solving skills to the next level!