The "standard form of circle" is a cornerstone concept in geometry and algebra, bridging the gap between theoretical mathematics and practical applications. Understanding this mathematical representation not only deepens your grasp of equations but also equips you with tools to solve real-world problems, from designing round objects to mapping celestial bodies. This guide will take you through everything you need to know about the standard form of a circle—its equation, applications, and much more.
From middle school to advanced mathematics, the standard form of a circle remains a key topic. It offers an algebraic way to describe the geometric properties of a circle, including its center and radius. Whether you're a student preparing for exams or someone intrigued by math, this guide simplifies the complexities of the concept, making it accessible to all. By breaking down the equation step by step, you’ll gain a concrete understanding of how it works and its uses.
In this comprehensive article, we’ll delve into the standard form of a circle, its derivation, and its applications. We’ll also tackle common questions like: What is the equation for the standard form of a circle? What are its real-life uses? Plus, you’ll find practical examples, visual illustrations, and FAQs to ensure you walk away with a complete understanding. Let’s get started on this mathematical journey!
Read also:Effective Ways To Remove Mold And Protect Your Home
Table of Contents
- What is the Standard Form of a Circle?
- Understanding the Standard Form Equation
- Why Do We Use the Standard Form?
- How to Derive the Standard Form of Circle?
- Components of the Standard Form Equation
- Differences Between Standard and General Form
- Transforming General to Standard Form
- Real-Life Applications
- Common Mistakes to Avoid
- Visualizing the Standard Form
- Frequently Asked Questions
- Conclusion
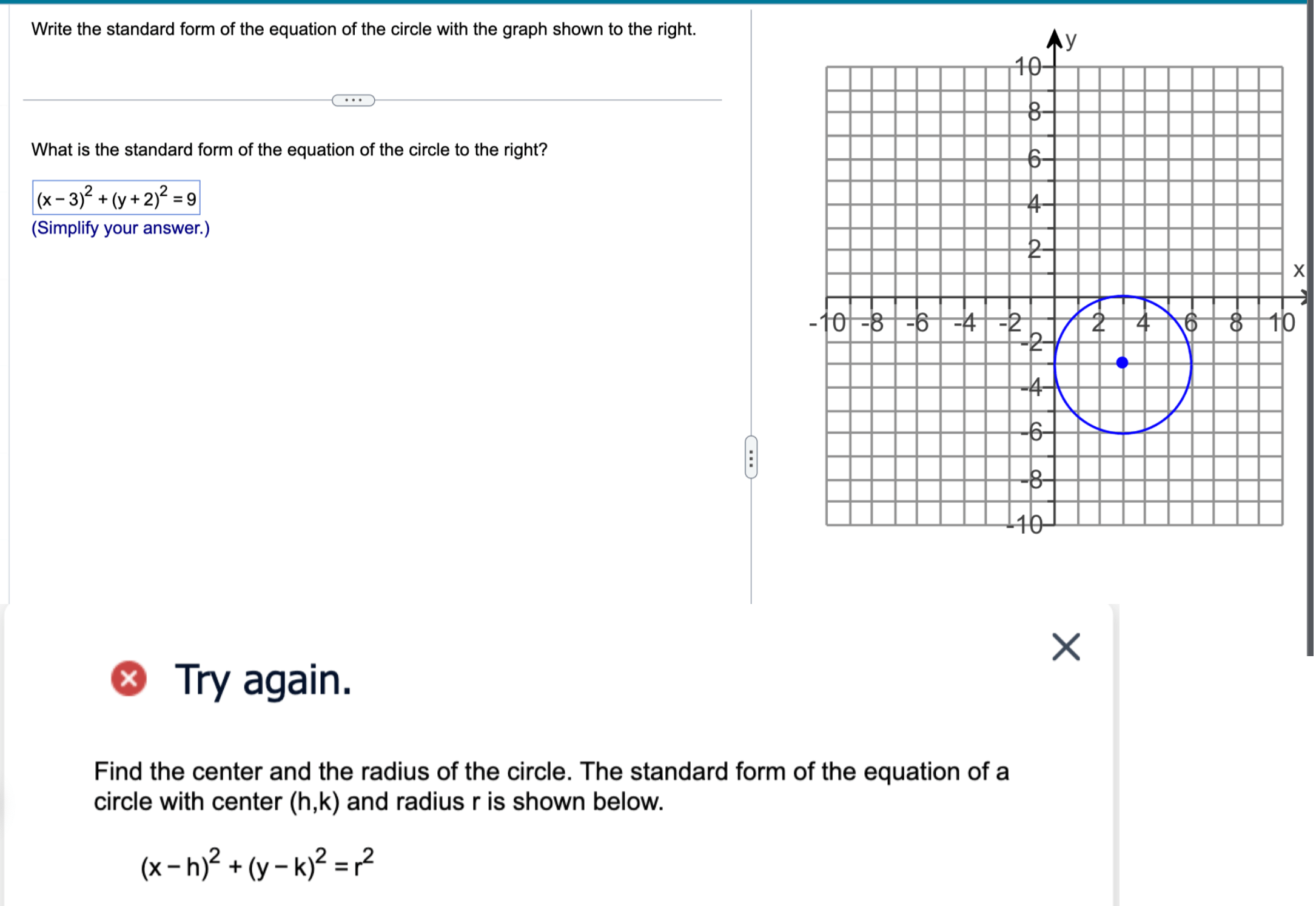
What is the Standard Form of a Circle?
The standard form of a circle is an algebraic equation that represents the geometric properties of a circle in a two-dimensional coordinate plane. This form is expressed as:
(x - h)2 + (y - k)2 = r2
Here’s what each component means:
- (h, k): The coordinates of the circle’s center.
- r: The radius of the circle.
- (x, y): Any point on the circle.
This equation succinctly captures the essence of a circle by showing the constant distance (radius) between the center and any point on the circle. It’s a versatile tool in geometry, physics, engineering, and other disciplines.
Understanding the Standard Form Equation
The equation (x - h)2 + (y - k)2 = r2 might look intimidating at first glance, but when broken down, it becomes straightforward.
Let’s dissect it:
Read also:Discovering The Heart Of Tempe Main Event In Focus
- (x - h)2: Represents the horizontal component of the circle.
- (y - k)2: Represents the vertical component of the circle.
- r2: The square of the radius, ensuring the equation remains quadratic.
In essence, the standard form equation tells us that the sum of the squares of the horizontal and vertical distances from the center equals the square of the radius. This balance is what defines a circle mathematically.
Why Do We Use the Standard Form?
The standard form of a circle is widely used for several reasons:
- Simplicity: It provides a clear and concise way to represent a circle’s geometry.
- Flexibility: Allows easy transformations and manipulations in algebraic problems.
- Visualization: Its components directly correspond to geometric features, making it easy to plot.
Moreover, the standard form is a foundation for advanced mathematical topics like conic sections and analytic geometry. It’s also practical in real-world applications such as satellite navigation and architectural design.
How to Derive the Standard Form of Circle?
The derivation of the standard form starts with the definition of a circle: a set of points equidistant from a fixed center. Suppose the center is (h, k), and the radius is r. For any point (x, y) on the circle, the distance to the center is r:
√((x - h)2 + (y - k)2) = r
Squaring both sides eliminates the square root:
(x - h)2 + (y - k)2 = r2
This is the standard form of a circle. It’s derived directly from the geometric definition and serves as a bridge between geometry and algebra.
Components of the Standard Form Equation
The Center of the Circle
The center of the circle is denoted as (h, k) in the standard form equation. It’s the fixed point from which all points on the circle are equidistant. The center plays a crucial role in determining the circle’s position on the coordinate plane.
The Radius of the Circle
The radius, represented by r, is the constant distance between the center and any point on the circle. It’s squared in the equation to maintain the quadratic nature of the formula.
Differences Between Standard and General Form
While the standard form of a circle is (x - h)2 + (y - k)2 = r2, the general form is:
Ax2 + Ay2 + Dx + Ey + F = 0
Key differences include:
- Simplicity: The standard form is more straightforward for identifying the circle’s center and radius.
- Utility: The general form is used in broader contexts, such as deriving equations of other conic sections.
Transforming General to Standard Form
To convert the general form to the standard form, follow these steps:
- Group x and y terms.
- Complete the square for both groups.
- Rearrange to match the standard form.
Real-Life Applications
The standard form of a circle is not just a theoretical concept. It has numerous real-world applications:
- Architecture: Designing circular structures like domes and wheels.
- Physics: Modeling orbits of celestial bodies.
- Technology: Algorithms for computer graphics.
Common Mistakes to Avoid
Some common pitfalls when working with the standard form include:
- Forgetting to square the radius.
- Mixing up h and k.
- Incorrectly completing the square.
Visualizing the Standard Form
Use graphing tools or software to plot the standard form of a circle. Visual aids help solidify your understanding and make complex concepts more tangible.
Frequently Asked Questions
1. What is the standard form of a circle equation?
The standard form of a circle equation is (x - h)2 + (y - k)2 = r2, where (h, k) is the center and r is the radius.
2. How do I find the radius from the standard form?
Take the square root of the constant on the right side of the equation (r2) to find the radius.
3. What are the applications of the standard form of a circle?
Applications include architecture, physics, navigation, and computer graphics.
4. Can the standard form represent an ellipse?
No, the standard form specifically represents a circle. An ellipse has a different equation.
5. What is the difference between standard and general form?
The standard form is simpler and directly shows the circle's center and radius, while the general form is more general and quadratic.
6. How do I convert the general form to the standard form?
Complete the square for x and y terms and rearrange to match the standard form.
Conclusion
The standard form of a circle is a fundamental concept in mathematics, offering a clear and concise way to represent circular geometry. From its derivation and components to its real-world applications, understanding this form equips you with valuable tools for both academic and practical purposes. Whether you’re solving equations or designing structures, mastering the standard form of a circle is an essential skill. Keep practicing, and this mathematical concept will become second nature.
Article Recommendations